In the previous part, we gave an overview of the Java Collection Framework, discussed the architecture, and discussed some of the implementation classes of the List interface and their internal mechanisms and use cases. If you missed it, please find it here.
In this part, we will discuss the rest of the Collection interface’s sub-interfaces, their implementation classes, and how they work internally.
Set
- Does not guarantee the order.
- Does not allow duplicate elements.
- Models the mathematical set abstraction
- Key methods include– add(E e) (which returns false if the element already exists), and contains(Object o).
Use Case
Used when the uniqueness of the elements is an essential requirement.
Implementation Classes
a) HashSet: Offering constant time performance for basic operations like add, remove, and contains.
Internal Mechanism
- Backing Structure: HashSet is implemented using a hash table, specifically a HashMap, where each element is stored as a key in the map with a constant value.
- Hashing: When adding an element, its hashcode is calculated using the hashCode() method to determine its index in the underlying array, allowing for efficient storage and retrieval.
- Collision Handling: If two elements hash to the same index, HashSet uses chaining to store multiple elements at that index in a linked list (singly-linked list) or a balanced tree (if the number of elements exceeds a threshold).
- Dynamic Resizing: The HashSet has an initial capacity and a load factor (default 0.75). When the number of elements exceeds the product of the current capacity and load factor, the hash table is resized (typically doubled), and elements are rehashed.
- Unique Elements: HashSet ensures all elements are unique, leveraging the equals() method to check for duplicates during insertion.
b) LinkedHashSet: Hash table and linked list implementation of the Set interface, with predictable iteration order.
Internal Mechanism
- This implementation differs from HashSet in that it maintains a doubly-linked list (instead of a singly-linked list) running through all of its entries. This linked list defines the iteration ordering, which is the order in which elements were inserted into the set (insertion order). An insertion order is unaffected if an element is re-inserted into the set.
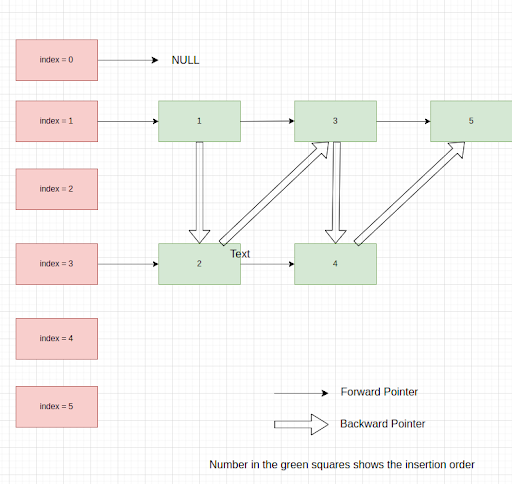
- LinkedHashSet uses a HashMap for efficient element storage and retrieval and a doubly-linked list to maintain insertion order. Each bucket in the hash table contains a linked list of entries (connected using FP), and each entry links to its position (insertion order) in the linked list (through BP).
- Performance: Offers average O(1) time complexity for operations (add, remove, contains) and O(n) for iteration with predictable order.
- Iteration: Iterates over elements in the order (BP) in which they were inserted.
- Use Case: LinkedHashSet is suitable for use cases where maintaining insertion order is essential and fast lookups are required. However, it uses more memory than HashSet due to the additional linked list that tracks insertion orders.
c) TreeSet: A sorted, non-thread-safe Set implementation that allows for efficient operations such as adding, removing, and checking for the presence of elements.
Internal Mechanism
- TreeSet internally uses a red-black tree (a balanced BST) to store elements in a sorted order to ensure efficient operations. The red-black tree maintains balance through specific properties and rebalancing techniques after insertions and deletions. Elements are sorted in a natural order (by Comparable interface) or by a provided comparator.
Example 1: Creating TreeSet with a custom type that implements Comparable
import java.util.TreeSet;
public class Person implements Comparable<Person> {
private String name;
private int age;
public Person(String name, int age) {
this.name = name;
this.age = age;
}
@Override
public int compareTo(Person other) {
// Sort by age, then by name if ages are the same
int ageComparison = Integer.compare(this.age, other.age);
if (ageComparison != 0) {
return ageComparison;
}
return this.name.compareTo(other.name);
}
@Override
public String toString() {
return "Person{name='" + name + "', age=" + age + "}";
}
public static void main(String[] args) {
TreeSet<Person> people = new TreeSet<>();
people.add(new Person("Alice", 30));
people.add(new Person("Bob", 25));
people.add(new Person("Charlie", 30));
// The elements will be sorted by age first, then by name
for (Person person : people) {
System.out.println(person);
}
}
}
Output:
Person{name='Bob', age=25}
Person{name='Alice', age=30}
Person{name='Charlie', age=30}
Example 2: Creating TreeSet using a Comparator
import java.util.Comparator;
import java.util.TreeSet;
public class Person {
private String name;
private int age;
public Person(String name, int age) {
this.name = name;
this.age = age;
}
@Override
public String toString() {
return "Person{name='" + name + "', age=" + age + "}";
}
public static void main(String[] args) {
// Create a TreeSet with a custom comparator
TreeSet<Person> people = new TreeSet<>(new Comparator<Person>() {
@Override
public int compare(Person p1, Person p2) {
// Sort by name, then by age if names are the same
int nameComparison = p1.name.compareTo(p2.name);
if (nameComparison != 0) {
return nameComparison;
}
return Integer.compare(p1.age, p2.age);
}
});
people.add(new Person("Alice", 30));
people.add(new Person("Bob", 25));
people.add(new Person("Charlie", 30));
// The elements will be sorted by name first, then by age
for (Person person : people) {
System.out.println(person);
}
}
}
Output:
Person{name='Alice', age=30}
Person{name='Bob', age=25}
Person{name='Charlie', age=30}
If you do not implement the Comparable interface or provide a Comparator, you will get an error like the following one:
Exception in thread "main" java.lang.ClassCastException: class Main$Person cannot be cast to class java.lang.Comparable
When to use Comparator
Here are scenarios where you will need to use a Comparator instead of a Comparable:
- Immutable or Third-Party Classes: You cannot modify the class to implement Comparable.
- Multiple Sorting Orders: You need to sort objects differently.
Performance: Operations like adding, removing, and checking elements run in O(log n) time due to the balanced nature of the red-black tree.
Use Case: Compared to other set implementations, it is helpful for efficient range queries (as it doesn’t require iterating over all items) and chronological task scheduling.
Queue
- Designed for holding elements before processing.
- Typically, order elements in a FIFO manner.
- Supports operations that allow elements to be inserted and removed at both ends.
Implementation Classes
a) LinkedList: A queue implementation that uses the LinkedList class to maintain a First-In-First-Out (FIFO) order for its elements.
Internal Mechanism
- A LinkedList-based Queue implementation that internally uses a doubly-linked list to ensure efficient FIFO operations. Elements are inserted at the tail and removed at the head, resulting in constant time complexity for enqueue and dequeue operations.
- Each node (element) contains data and references to the next and previous nodes, facilitating dynamic resizing.
Use Cases: While it uses more memory than array-based queues due to node pointers, it’s a better option for Queues. When we remove an element from the beginning of an array, it actually rearranges the elements. But there needs to be rearrangement in LinkedList.
b) PriorityQueue: A queue implementation that orders the elements according to a specified comparator.
Internal Mechanism
- It is implemented using a binary heap, either min-heap (default) or max-heap, to retrieve the highest (or lowest) priority element efficiently. Elements are ordered based on their natural ordering or a provided Comparator. Insertion and removal operations (offer, poll) maintain the heap property through “bubbling up” (moving a newly added element upwards by swapping with the parent) and “bubbling down” (moving a freshly added element downwards by exchanging with the child) both with O(log n) time complexity (you can easily derive this time complexity using the relation between the number of nodes and the height of the heap). PriorityQueue dynamically resizes its internal array (uses an array to implement the heap) as elements are added or removed, ensuring efficient memory usage.
// Create a min-heap
PriorityQueue<Integer> minHeap = new PriorityQueue<>();
// Create a max-heap using a custom comparator
PriorityQueue<Integer>maxHeap = new PriorityQueue<>(Comparator.reverseOrder());
Use Cases: Commonly used for task scheduling, resource management, and algorithms requiring prioritized processing, such as Dijkstra’s algorithm.
Deque
A linear collection that allows insertion and removal of elements at both ends. Deque and LinkedList can be used for similar purposes but have distinct roles and advantages. Deque provides a straightforward and dedicated API for deque operations.
- It can be either capacity-restricted (array) or have no fixed size limit (linked list).
- Provides methods to access elements at both ends, with each method available in two forms: one that throws exceptions and another that returns an exceptional value on failure.
Use Case
- Double-ended Queue: Efficient for FIFO and LIFO operations.High Performance: Ideal for high-performance scenarios needing constant-time insertions and removals from both ends.
- Buffering/Caching: This is useful for buffering data and implementing sliding windows (due to its ability to add and remove elements from both ends efficiently).
- Undo/Redo: This feature supports maintaining history for undo/redo functionality (using two different deques for undo and redo).
- Graph Algorithms: Suitable for BFS and other algorithms requiring access to both ends of a collection.
Implmenetation Classes
a) ArrayDeque: ArrayDeque is an array implementation of the Deque (double-ended queue) interface.
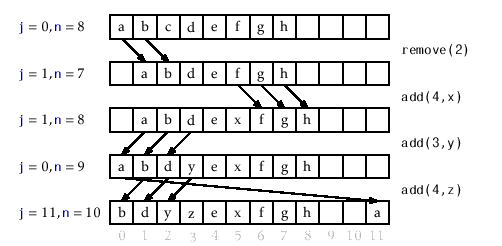
ArrayDeque internally uses a circular array. Thus, it uses the space efficiently and allows quick access and modification at both ends of the deque. It maintains pointers to the head and tail, updating them as elements are added or removed.
It wraps around indices when they exceed bounds. When the array becomes full, it automatically resizes, typically doubling its size, and copies the existing elements to the new array.
Performance: Provides amortized constant-time operations for adding and removing elements, with efficient space utilization.
b) LinkedList: The LinkedList class in Java implements the List and Deque interfaces using a doubly linked list. It supports all optional list operations (not strictly required by the core List interface but is part of the List interface’s extended capabilities), such as addAll(Collection<? extends E> c), and allows null elements.
In this implementation, operations that access elements by index will start from the end of the list or the beginning, whichever is closer to the specified index.
Internal Mechanism
- Doubly Linked List: Uses nodes with data, next, and previous references.
- Head and Tail: Maintains pointers to the first and last nodes for efficient end operations.
- Operations: Adding/removing elements from both ends is done constantly, O(1).
- Access: Due to traversal, indexed access requires linear time, O(n).
- Memory: Each node has additional memory overhead for pointers, and the list dynamically adjusts its size.
Conclusion
This concludes the second part of the Java Collection Framework. Here, we have discussed the rest of the Collection interface’s sub-interfaces, their implementation classes, and how they work internally.
In the next part, we will discuss the Map interface and its implementation classes, including how they work internally and the use cases.