Binary trees, a cornerstone of computer science, offer a versatile solution for storing, accessing, and manipulating hierarchical data. Their applications span a wide range, from serving as syntax trees in compilers to forming the backbone of heap structures in algorithms.
In this blog, we’ll explore the basic structure of binary trees, how memory is allocated when working with them, and walk through a Preorder Traversal method.
What is a Binary Tree?
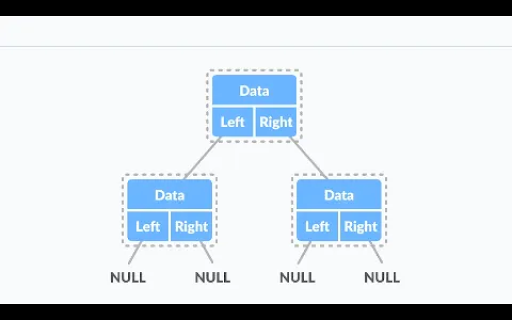
A binary tree is a hierarchical, non-linear data structure where each node can have at most two children: a left child and a right child. Each node consists of three parts:
- Data: The value the node holds.
- Left Child: A reference to the left child node.
- Right Child: A reference to the right child node.
Class Node{
int data;
Node left;
Node right;
public Node(int value) {
data = value;
left =right = null;
}
}
Applications of Binary Trees
Binary trees find practical use in a variety of fields. Power-efficient data access in databases guides routers in determining optimal data paths and underpins the construction of heaps for priority queues. They even play a crucial role in the syntax trees used by compilers.
- Efficient Data Access: Binary search trees are useful in databases because they allow for quick lookups, insertions, and deletions.
- Router Algorithms: Routers often use binary trees to determine the most efficient path for data packets.
- Heap Construction: Heaps are complete binary trees used to implement priority queues, which are fundamental in tasks like scheduling.
- Syntax Trees: Compilers use binary trees to parse expressions and generate code.
This code snippet shows the node structure with data left and right.
The structure of a binary tree, with its nodes and their references, is an elegant solution for storing and managing hierarchical data. Understanding how this structure is allocated in memory adds another layer of fascination to this data structure.
Let’s dive deeper into how binary trees are structured in memory. Each node in the tree exists in heap memory because it is dynamically allocated, while references to these nodes are stored in the stack memory. The root node is stored in the heap, and each time we add a new node, the system also allocates memory for that node on the heap.
public class BinaryTree {
Node root;
public BinaryTree(int key) {
root = new Node(key);
}
public BinaryTree() {
root = null;
}
}
When we create a new BinaryTree object, its root reference is stored in stack memory. However, the actual node is created in heap memory. As we add more nodes, the references to these nodes are kept in the tree structure, while the nodes are stored in the heap.
Building a Binary Tree
Let’s look at a complete binary tree example. Below is a Java code snippet that creates a binary tree with seven nodes:
public static void main(String[] args){
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
tree.root.right.left = new Node(6);
tree.root.right.right = new Node(7);
}
In this code:
- We create the binary tree and add nodes to form the following structure:
/**/
1
/ \
2 3
/ \ / \
4 5 6 7
Traversal Process
As we know, the three most common tree traversal approaches are-
- Preorder traversal
- Inorder traversal
- Postorder traversal
In one of my blogs, I may discuss three of these traversal methods. In this blog, I will show just one method for traversing a binary tree.
public void printPreOrderTraversal(Node node) {
if (node != null) {
System.out.print(" " + node.data + "->");
printPreOrderTraversal(node.left);
printPreOrderTraversal(node.right);
}
}
}
These code snippets traverse the whole binary tree using recursion. This code will print the value in PreOrder Traversal. The result will print:
1-> 2-> 4-> 5-> 3-> 6-> 7->
Now, our full code snippets look like :
package BinaryTree;
class Node{
int data;
Node left, right;
public Node(int value) {
data = value;
left = right = null;
}
}
public class BinaryTree {
Node root;
public BinaryTree(int key) {
root = new Node(key);
}
public BinaryTree() {
root = null;
}
public static void main(String[] args) {
BinaryTree tree = new BinaryTree();
tree.root = new Node(1);
tree.root.left = new Node(2);
tree.root.right = new Node(3);
tree.root.left.left = new Node(4);
tree.root.left.right = new Node(5);
tree.root.right.left = new Node(6);
tree.root.right.right = new Node(7);
tree.printPreOrderTraversal(tree.root);
}
public void printPreOrderTraversal(Node node) {
if (node != null) {
System.out.print(" " + node.data + "->");
printPreOrderTraversal(node.left);
printPreOrderTraversal(node.right);
}
}
}
Memory Allocation Summary
In terms of memory:
- The stack memory holds the local variables, including the reference to the root node.
- The heap memory stores the actual Node objects for the tree.
- As we add nodes to the tree, the memory dynamically allocates new Node objects on the heap, while references to these objects are managed in the stack.
Conclusion
Binary trees are an essential data structure in numerous real-world applications, from search algorithms to compiler data parsing. In this post, we’ve covered the basics of binary trees, including their structure, how memory is allocated, and how to traverse them using Preorder Traversal.